Graph Terminology

Adjacent vertices :

        An adjacent vertex of a vertex v in a graph G is a vertex that is connected to v by an edge.

                                        ( or )

In simple if two vertices in an undirected graph are connected by an edge, then they are called as Adjacent vertices or Neighbors.

 fig 1

               

In fig1:

Adjacent vertices of a : b,c,e

Adjacent vertices of b : a

Adjacent vertices of c : a,d,e

Adjacent vertices of d : c,e

Adjacent vertices of e : a,c,d

·       But For an directed graph it is different .For example

Fig: 2

·       Here there is an edge between 3, 2 which is represented as  (3, 2) means 2 is adjacent to 3 but 3 is not adjacent to 2.

Predecessor and Successor :

       The vertex of which the arrow comes out is called Predecessor and the vertex that is pointing by the arrow is called Successor.

In Fig 2. Vertex 3 is the Predecessor and Vertex 1 is the Successor.

Degree of a Vertex :

        In graph theory, the Degree of a vertex of a graph is the Number of edges that are incident on that vertex.

·       If there is a loop, the edges of that loop is counted as twice.

·       The degree of a vertex v is denoted deg(v) or deg v.

·       The maximum degree of a graph G, denoted by Δ(G)

·       The minimum degree of a graph, denoted by δ(G)

Fig 3

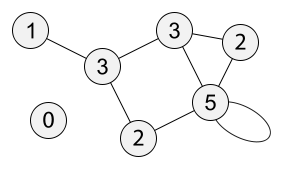
In the above fig.3, the degree of vertex 5 is 5

Terminology on vertex :

·       A vertex with degree 0 is called an Isolated vertex.

In the above fig.3, The degree of vertex 0 is 0.

Fig .4

·       A vertex with degree 1 is called a Leaf vertex or End vertex, and the edge incident with that vertex is called a Pendant edge. In the graph (fig 4) on the right, {3,5} is a pendant edge.

·       A vertex with degree n − 1 in a graph on n vertices is called a Dominating vertex.

In-degree and Out-degree :

In a directed graph it is important to distinguish between In-degree and Out-degree. For any directed edge, it has two distinct ends:  a head (the end with an arrowhead) and a tail. Each end is counted separately. The sum of head endpoints count toward the In-degree of a vertex and the sum of tail endpoints count toward the Out-degree of a vertex.

·       The In-degree of a vertex V written by deg −(v).

·       The Out-degree of a vertex V written by deg +(v)

For example :

Fig .5

·       vertex 2 has In-degree 2.

·       vertex 2 has Out-degree 1.

Question :

Find the In -Degree, Out-degree, and degree of each vertex of a graph given below.

Fig.6

In-Degree of a vertex 'v1' = deg(v1) = 1 and Out-Degree of a vertex 'v1' = deg(v1) = 2

In-Degree of a vertex 'v2' = deg(v2) = 1 and Out-Degree of a vertex 'v2' = deg(v2) = 3

In-Degree of a vertex 'v3' = deg(v3) = 1 and Out-Degree of a vertex 'v3' = deg(v3) = 2

In-Degree of a vertex 'v4' = deg(v4) = 5 and Out-Degree of a vertex 'v4' = deg(v4) = 0

In-Degree of a vertex 'v5' = deg(v5) = 1 and Out-Degree of a vertex 'v5' = deg(v5) = 2

In-Degree of a vertex 'v6' = deg(v6) = 0 and Out-Degree of a vertex 'v6' = deg(v6) = 0

·       By the definition, the degree of a vertex is Deg(v) = deg−(v) + deg+(v). Therefore

Degree of a vertex 'v1' = deg(v1) = 1 + 2 = 3

Degree of a vertex 'v2' = deg(v2) = 1 + 3 = 4

Degree of a vertex 'v3' = deg(v3) = 1 + 2 = 3

Degree of a vertex 'v4' = deg(v4) = 5 + 0 = 5

Degree of a vertex 'v5' = deg(v5) = 1 + 2 = 3

Degree of a vertex 'v6' = deg(v6) = 0 + 0 = 0