Associativity of operators

Associativity of operators :

In general, expressions are the combination of operands and operators. An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations. We have different types of operators which have some priority. According to priority, the expressions are simplified.

For example :

a * b + c;

                    Here, operands are  a, b, c and operators are *, +

      From the table, we see that  *  have high priority than  +. So the expression is equal to ((a * b) + c). This tells that the * operator is executed first and + next.

        If an expression contains two or more equal priority operators, then we have to use the Associativity of operators.

For example :

a * b + c / d - e

        Here operands are  a, b, c, d, e operators are * , + , / , -

        From the priority table we get  *  and  / have equal priority and also + and –  have equal priority.

      By this, We get the expression as (a * b) + ( c / d) - e. Now the problem arises which one should first to be executed ((a * b) + (c / d)) or ((c / d) - e) i.e. either  + or -. Associativity indicates in which order two operators of same precedence (priority) executes first.

For example :

              Suppose if we consider the expression  a == b != c ,

Operands are a, b, c and operators are  == , != . These two have same priority. The associativity of both == and != is left to right i.e. the expression in left is executed first and execution takes place towards right. Thus a == b != c is equal to ((a == b) != c)

             Now if we consider the above expression,  As arithmetic operators have left to right precedence, expression which is on the left is solved first i.e. ((a * b) + (c / d)) and final expression is (((a * b ) + ( c / d )) - e).

Different types of Operators :

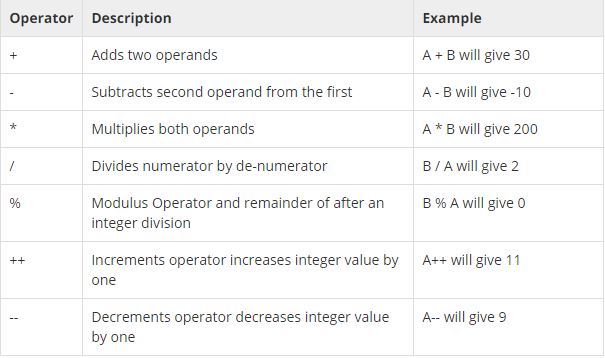
1) Arithmetic Operators :

if A = 10 and B =20

2) Relational Operators :

3) Logical Operators :

4) Bitwise Operators :

5)  Assignment Operators :

6) Misc Operators :

Precedence of operators :
 

From the above table , we see that only only Unary , Conditional and some of Assignment operators are having associativity Right to Left. Remaining are Left to Right associative. So its better to have glance at operators having Right to Left associativity.